4.2 Directed Graphs

A directed graph (or digraph) is a set of vertices and a collection of directed edges that each connects an ordered pair of vertices. We say that a directed edge points from the first vertex in the pair and points to the second vertex in the pair. We use the names 0 through V-1 for the vertices in a V-vertex graph.

Glossary.

• A self-loop is an edge that connects a vertex to itself.
• Two edges are parallel if they connect the same ordered pair of vertices.
• The outdegree of a vertex is the number of edges pointing from it.
• The indegree of a vertex is the number of edges pointing to it.
• A subgraph is a subset of a digraph's edges (and associated vertices) that constitutes a digraph.
• A directed path in a digraph is a sequence of vertices in which there is a (directed) edge pointing from each vertex in the sequence to its successor in the sequence, with no repeated edges.
• A directed path is simple if it has no repeated vertices.
• A directed cycle is a directed path (with at least one edge) whose first and last vertices are the same.
• A directed cycle is simple if it has no repeated vertices (other than the requisite repetition of the first and last vertices).
• The length of a path or a cycle is its number of edges.
• We say that a vertex w is reachable from a vertex v if there exists a directed path from v to w.
• We say that two vertices v and w are strongly connected if they are mutually reachable: there is a directed path from v to w and a directed path from w to v.
• A digraph is strongly connected if there is a directed path from every vertex to every other vertex.
• A digraph that is not strongly connected consists of a set of strongly connected components, which are maximal strongly connected subgraphs.
• A directed acyclic graph (or DAG) is a digraph with no directed cycles.

Digraph graph data type.

The key method adj() allows client code to iterate through the vertices adjacent from a given vertex.

We prepare the test data tinyDG.txt using the following input file format.

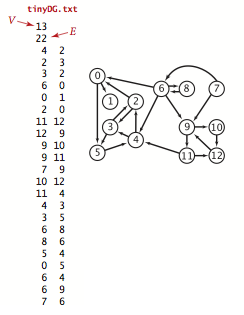
Graph representation.

We use the adjacency-lists representation, where we maintain a vertex-indexed array of lists of the vertices connected by an edge to each vertex.

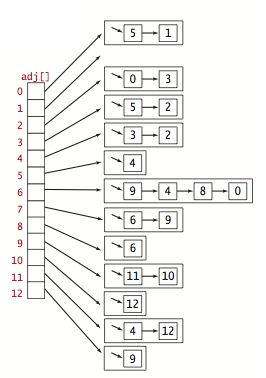
Digraph.java implements the digraph API using the adjacency-lists representation. AdjMatrixDigraph.java implements the same API using the adjacency-matrix representation.

Reachability in digraphs.

Cycles and DAGs.

Directed cycles are of particular importance in applications that involve processing digraphs. The input file tinyDAG.txt corresponds to the following DAG: