
Here’s the understatement of the year: teaching place value is kind of a big deal! From kindergarten through 5th grade, “Numbers and Operations in Base Ten” shows up in the common core math standards like clockwork.
The task of “understanding place value” grows in complexity every year and really ramps up starting in 3rd grade. Students are expected to learn how to “fluently add and subtract within 1000” using number-sense strategies based on place value. This 3-digit math strategy can feel uncomfortably like the big leagues for kids struggling with place value. So I’m going to share:

Before I share 3 tips, let’s build some background. Students as early as kindergarten and 1st grade come to school knowing things about two digit numbers like how to verbally count from 10 to 100 and counting objects within 15 or 20.
However, their understanding of numbers is pretty different from ours in that it’s based on a counting by ones approach. So they typically count one thing at a time and don’t readily understand the connection between a number and the groups of tens and ones.
For example, if we ask a student how many tens are in 67. They may say 6 in the tens place because they simply name the position with little understanding of it. But they may not understand that 6 represents 6 groups of ten things and 7 represents 7 single things. Understanding that a group of ten can represent a single entity is a huge shift!
Students tend to struggle because understanding place value is anything but simple. It’s all a big puzzle where three big pieces or connections should be made.
The first key is understanding base-ten concepts in order to represent numbers visually. While many teachers may provide students opportunities to represent numbers using standard groupings, it’s equally as important for students to represent numbers using equivalent groupings. I consider this to be the keystone of place value.
Students should also be able to articulate numbers in their oral forms, whether they’re standard (“seventy-two”) or base-ten (“7 tens and 2 ones”).
Finally, students have to understand how to read and write numerals. Making these three connections hinges on utilizing different counting strategies in practice: counting by ones, counting by groups and singles, and counting by tens and ones.
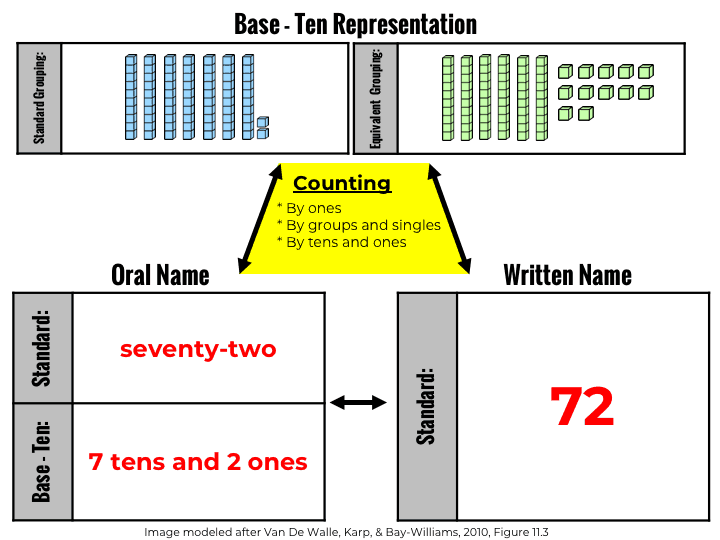
See how all of this works together? If students miss one piece, then it would be challenging for them to have a full understanding of place-value. That’s why giving kids the right tools to understand the place value system is so important.
Here are a few tips that develop place value:
Yes, manipulatives are great for moving students from concrete understanding to abstract. Place value mats work nicely with manipulatives by helping to drive abstract concepts home.
Help struggling learners by making learning hands-on and visual. That means using manipulatives like base-ten blocks. Base-ten blocks are the best tool on the block – pun intended. A great thing about base-ten blocks are the versatility to build whole numbers or decimals.
With the unit block representing one, allow students time to explore the relationship between the units (small block) and rods as well as the rods and a flat on a place value mat. Exploring these relationships support the 10- to- 1 relationship of place value including: 10 units equal 1 ten, 10 tens equal 1 hundred and so on.

Warning: Base ten blocks are all about relationships. Each block can represent different amounts depending on how they’re used. Don’t make your kids think that each block can ONLY represent one thing. For example, when using base ten blocks to represent decimals, the flat may represent 1 and the smallest block may represent 1 hundredth. When talking to kids, I find it easy to use the phrase: In this situation __________ represents __________.
Now let’s talk place value charts. Create simple place value charts that are reusable by including a place for hundreds, tens, and ones. This layout mimics the way the number is written from left to right. In the ones section, ensure that there are two ten-frames to promote the concept of a group of ten and eliminate the need for one-by-one counting. Ten frames also help students visualize how many more units are needed to make a complete set of ten.
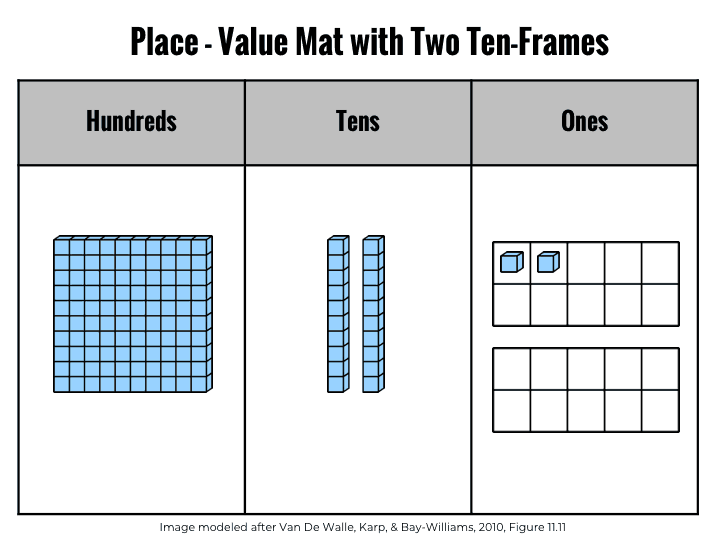
Also give students time to represent a number using standard groupings and equivalent groupings. For example, the numeral 49 can be represented in standard form as 4 tens and 9 ones.
 with base ten blocks " width="711" height="532" />
with base ten blocks " width="711" height="532" />
As well use equivalent groupings of 49 to show 3 tens and 19 ones. Without these types of experiences kids really struggle understanding that both values are equivalent.
 with base ten blocks " width="711" height="540" />
with base ten blocks " width="711" height="540" />
You may have kids in 2nd and 3rd grade that continue to count things by ones instead of groupings things by 10. Grouping by 10’s is important because it’s mentally easier to count plus our number system is based on 10’s! Since we want to foster students ability to count by 10’s (not impose it on them) check out these 2 helpful activities.
The Crayon Counting Challenge
Gather your students in a circle. Find a collection of crayons (or any countable items ranging from 25 to 100) and spill them out in the middle of the circle. Ask students, “How could we can count these crayons in a way that’s easier than counting by ones?” Test out any of the counting suggestions that students give (ie. if they say count by 3’s then group and count the crayons by threes until you can’t make any more groups of 3).
After testing different strategies have a discussion on what worked well and what didn’t work so well. If no one suggests the idea of counting by 10’s, suggest it to the group and discuss how it worked in comparison to the other counting suggestions. Students typically discover that counting by 5’s or 10’s is the easiest method to group and count items.

The Classroom Estimation Activity
Create an estimation jar in your class. Fill a durable, clear plastic jar with 200 to 1000 items. Items like tiny erasers, beans or paper clips work well and are pretty inexpensive.
First give all students an opportunity to write down their estimates of the number of items in the jar. For example below, every student would record the number of erasers they believe are in the jar. After students arrive at their estimates have a class discussion about strategies they used to arrive at their recorded amount.

Next pour out all the items (ie. erasers) into several cups.
Group students in pairs and provide them with a cup to count and group the items 10 at a time.

After students have grouped all items into 10’s, place all of the groups in front of the class and ask the following questions:
After the class discussion provide larger containers for the new groups. For example, students may form new groups of 50 or 100 by combining 5 cups of 10 erasers into one container of 50. Make sure that you have large enough containers for the new groups (ie. 50 erasers in each new group) and label each new group.
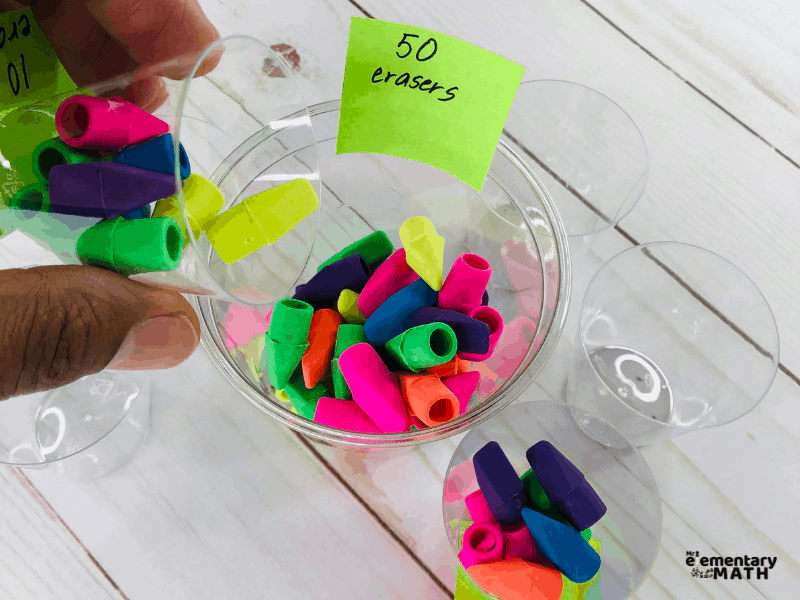
Once all of the new groups are formed, count the hundreds, tens and ones separately. Record the total number of items (erasers) on a sheet of paper and discuss how their estimates were similar to or different from the actual number counted.
Another great strategy for reinforcing place value is a daily warm-up, especially if it incorporates math talk. Since place value and base 10 understanding are the basis of our number system, it’s important that students get plenty of practice.
You’ve probably heard that people need to do something for 30 days to make it a habit. The same holds true for kids. To help your students master place value, I’ve created a 30 day warm- up routine. This routine engages your class in meaningful math discussions while building place value understanding within 1000.
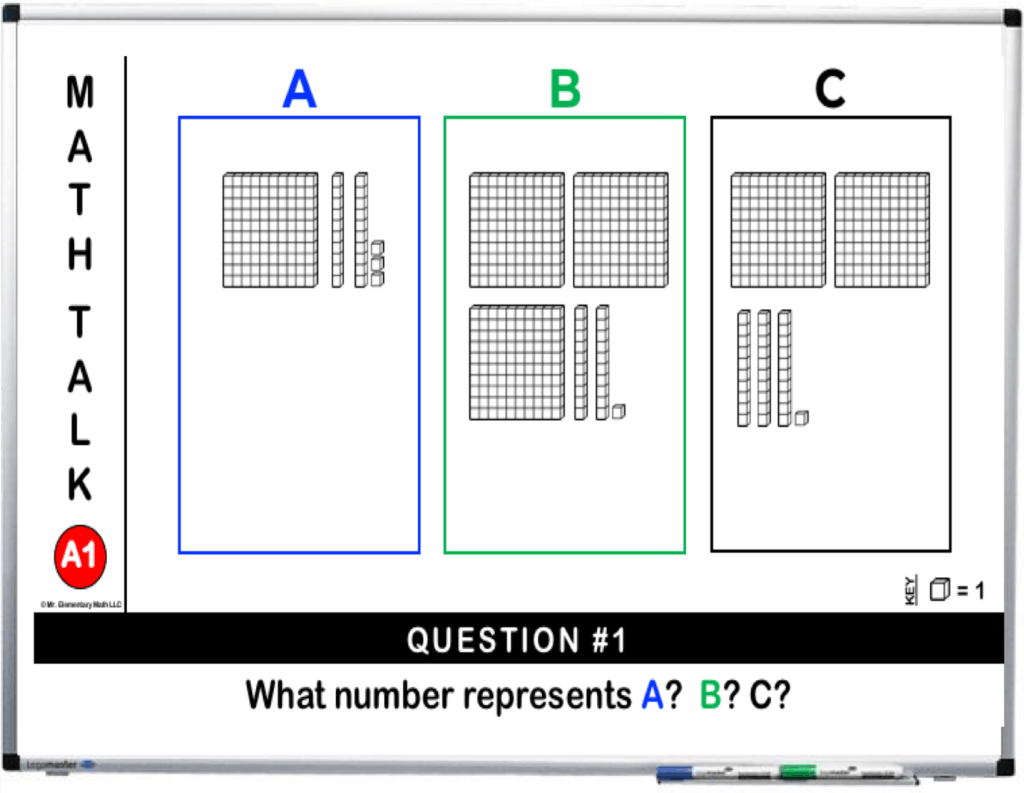
Each day, project one math talk lesson onto your interactive whiteboard. Students will complete 4 daily questions. With 3 levels and 10 math talk activities included in each level, you’ll have 30 days of place value learning.
Level A: Beginner
Includes 10 math talks with:
Level B: Intermediate
Includes 10 math talks with:

Level C: Advanced
Includes 10 math talks with:

Take your student understanding of place value to the next level using this routine. Click on the image below to purchase.